
Das vor 150 Jahren entdeckte Ohmsche Gesetz fand ein Teilverständnis kurz nach der Jahrhundertwende und kann nach Abschluß der Quantenmechanik als verstanden gelten.
Wir schreiben es als Beziehung zwischen Spannung und Stromstärke:
\begin{align}U=\rho\ \frac{1}{q}\ J\end{align}
oder zwischen elektrischer Feldstärke und Stromdichte (isotropes Material vorausgesetzt):
\begin{align}E=\rho\ i\end{align}
wo $\rho$ eine Stoffeigenschaft bezeichnet. Es hat drei bemerkenswerte Eigenschaften:
Wir wollen sehen, wie weit wir diese drei Eigenschaften verstehen.
Sie kann bedeuten, daß wir es mit einem einfachen Vorgang oder mit einer Näherung für kleine Größen zu tun haben. Das zweite ist der Fall. Zwar wird die Vakuumelektrodynamik mit den linearen Maxwellschen Gleichungen beschrieben; aber die elektrischen Vorgänge in der Materie sind komplex. Also ist das Ohmsche Gesetz wohl eine lineare Näherung. Bei Metallen gilt es aber recht genau. Sind die in (2) vorkommenden Größen wirklich klein? Wir müssen zuerste fragen, wogegen klein? Gibt es naturgegebene universelle Maßstäbe? Die klassische Mechanik ist skaleninvariant; man kann die Massen, Längen, Zeiten je mit einem willkürlichen Faktor multiplizieren, die Gleichungen bleiben dieselben. Die gebräuchlichen Einheiten kg, m, s beruhen auf Eigenschaften unseres speziellen Planeten Erde. Die Stoffeigenschaften jedoch deuten auf naturgegebene universelle Einheiten hin; eine Theorie der Stoffe kann nicht skaleninvariant sein. Für die Atomhüllen und damit die meisten Stoffeigenschaften sind die natürlichen Einheiten $m$, $e$, $h$, Masse des Elektrons, elektrische Elementarladung und elementares Wirkungsquantum; $m$ und $e$ sind Eigenschaften des Modells, das wir uns vom Atom machen; $h$ ist die Größe, die die anschauliche Beschreibbarkeit einschränkt und damit das Atom denkmöglich macht. Die wichtigsten aus $m$, $e$, $h$ abgeleiteten "atomaren" Einheiten sind (sehr abgerundet) die Länge 0,5⋅10-10 m, die Zeit 2⋅10-17 s, die Temperatur 3⋅105 K, die elektrische Spannung 27 V, die elektrische Feldstärke 5⋅1011 V/m und die Stromdichte 2⋅1018 A/m2 oder 2⋅1012 A/mm2.
Beim Experimentieren mit Metallen sind die vorkommenden Stromdichten sehr klein verglichen mit 2⋅1012 A/mm2 und die Feldstärken sehr klein gegen 5⋅1011 V/m. Die Linearität des Ohmschen Gesetzes ist darum verständlich.
Für den spezifischen Widerstand $\rho$ ist die atomare Einheit 2⋅10-7 Ωm, das entspricht einem Ohm bei einem Draht von 1 mm2 Querschnitt und 5 m Länge. Die wirklichen Widerstände der Metalle bei Zimmertemperatur sind von dieser Größenordnung. Ein Ohm wird bei 1 mm2 Querschnitt dargestellt durch einen Quecksilberfaden von 1 m Länge, einen Eisendraht von 10 m Länge, einen Silberdraht von 70 m Länge. Die genäherte Übereinstimmung mit der atomaren Einheit hat aber keinen einfachen Grund.
Dem nicht durch Physik verdorbenen Menschen erscheinen nicht umkehrbare Vorgänge als die natürlichen. Die aristotelische Bewegungslehre, die eine Physik des Augenscheins war, gelangte zu dem Gesetz $F \propto Rv$ zwischen Antrieb, Widerstand und Geschwindigkeit für natürliche und gewaltsame Bewegungen; das Gesetz ist nicht invariant gegen Zeitumkehr; die natürlichen Bewegungen galten als Ausgleich eines unnatürlichen Zustandes. Das Ohmsche Gesetz ist von diesem Typus; es handelt von einem Ausgleichsvorgang, einem Vorgang, bei dem die Reibung wichtig und die Trägheit zu vernachlässigen ist. In der Optik sehr guter Leiter benutzt man das allgemeinere Gesetz
\begin{align*}E=\frac{{\rm d}i}{{\rm d}t} + \rho\ i\end{align*}
bei Supraleitern fällt das zweite Glied der rechten Seite fort. Bei sehr guten Leitern überwiegt der Einfluß der Trägheit, bei gewöhnlichen Leitern der Einfluß einer Reibung.
Das Ohmsche Gesetz ist ein Grenzgesetz nicht nur für die kleinen Feldstärken und Stromdichten, sondern auch für die vorkommenden nicht kleinen Widerstände.
Für die heutige Physik sind die Grundgesetze invariant gegen Zeitumkehr. So kommt es zu der Frage: wie folgt ein nicht zeitumkehrinvariantes Gesetz, wie das Ohmsche, aus zeitumkehrinvarianten Grundgesetzen? Nun, der Physiker versteht das als Übergang in einen wahrscheinlicheren Zustand. Ersetzen wir (ohne wesentliches zu ändern) die Elektrizitätsleitung bei konstanter Spannung, die ein Fließgleichgewicht ist, durch den Spannungsausgleich zwischen zwei begrenzten Leitern, die durch einen dünnen Draht verbunden seien, also durch einen Vorgang, der einem Gleichgewicht zustrebt. Wir haben dann ziemlich das Gleiche wie den Druckausgleich des Gases in zwei Kammern, die durch eine enge Öffnung verbunden sind. Nehmen wir zwei gleiche Kammern an und beginnen wir mit einer leeren Kammer, also den Molekelzahlen $N_1 = 0$. $N_2 = N$, so wird $N_1(t)$ bei kleiner Zahl $N$ etwa durch die Abb. 1 wiedergegeben. $N_1$ bleibt in der Nähe von $N/2$. Vom ersten Anfang abgesehen, ist der Verlauf (statistisch genommen) symmetrisch in den beiden Zeitrichtungen. Wenn eine merkliche Schwankung auftritt, so erwarten wir, daß sie sich nach der Zukunft hin abnimmt und in der Vergangenheit entsprechend zugenommen hat.

Man kann die Vorgänge durch "Entropiespiele" (etwa das Ehrenfestsche Urnenspiel) simulieren und so völlig durchsichtig machen; die Änderungen gehen dann in diskreten Schritten. Wahrscheinlich ist dann für die Zukunft eine Änderung:
\begin{align*}\Delta N \propto N_2 - N_1\end{align*}
\begin{align*}\Delta (N_1 - N_2) \propto -2(N_1 - N_2),\end{align*}
also ein Verlauf der Differenz
\begin{align*}\dot\xi \propto - \xi .\end{align*}
Für die Vergangenheit (wenn man sie nicht zur Kenntnis genommen hat) gilt
\begin{align*}\dot\xi \propto + \xi .\end{align*}
Die Schwankungen zeigen keine Unsymmetrie bezüglich der beiden Zeitrichtungen. Über eine größere Schwankung wundern wir uns, und wir wenden dann für die Zukunft den zweiten Hauptsatz der Theorie der Wärme an. Ganz große Abweichungen vom Gleichgewicht (wie den Anfang der Abb. 1) sehen wir als künstlich hergestellt an oder als unbegreifbare Eigenschaft unserer Welt.
Die Irreversibilität von Vorgängen beruht auf ausgefallenen Anfangsbedingungen. Der Zweite Hauptsatz gilt, weil die Welt in einem sehr unwahrscheinlichen Zustand ist, also auf einem kosmologischen Faktum, das wir physikalisch nicht verstehen.
Die Reversibilität kleiner Schwankungen wird bei der Ableitung der Onsagerschen Relationen benutzt. Solange für Ausgleichsvorgänge noch lineare Sätze gelten (wie für die elektrische und thermische Leitfähigkeit), behandelt man sie wie Folgen kleiner Schwankungen. So ist die Theorie komplizierter Transportvorgänge in Materie ein Tummelplatz für die Onsagerschen Relationen, und es gibt einen Zweig, den man "linear response theory" nennt.
Die Erfahrung zeigt uns Isolatoren, Halbleiter, Metalle; bei den letzteren ist der spezifische Widerstand $\rho$ ungefähr der Temperatur proportional. Bei verschiedenen Stoffen ist verschieden; bei Ag, Cu, Al ist $\rho$ gering, bei Fe groß. Woher kommt der Widerstand? Worin besteht die Reibung?
Etwa um die Mitte der Zeit zwischen Ohms Entdeckung und heute gelang ein Teilverständnis mit einem einfachen Modell: Im Metall bewegen sich Elektronen und stoßen gelegentlich auf Hindernisse, unterliegen so einer Art Reibung. Unterscheidet man eine mittlere Geschwindigkeit $u$ der Elektronen in der Richtung des Stromes und eine mittlere Geschwindigkeit $v$ ihrer ungeordneten Bewegung, die sie während einer Zeit $l/v$ ausführen, die durch eine mittlere Weglänge $l$ begrenzt ist, so läßt sich bei $n$ Elektronen in der Raumeinheit die Stromdichte als
\begin{align*}i=-e\ n\ u\end{align*}
schreiben und $u$ als Folge der elektrischen Kraft ansehen:
\begin{align*}m\ u =-e\ E\ \frac{l}{v}\end{align*}
Man erhält so
\begin{align}\rho = \frac{m\ v}{e^2 n l}\end{align}
d.h. eine einfache Abhängigkeit von $n$, $l$, $v$. Wenn man eine feste Zahl von Leitungselektronen annimmt, wird 1/$n$ dem Atomvolumen Ω proportional. Die empirischen $\rho$-Werte nehmen, grob gesprochen, bei chemisch ähnlichen Metallen mit dem Atomvolumen zu. Cu, Ag, Au sind sehr gute Leiter, in der Reihe Na, K, Rb, Cs nimmt der spezifische Widerstand zu. Wenn man jedoch, den damaligen Anschauungen entsprechend, für $l$ den Atomabstand $\propto \Omega^{1/3}$ und $v^2 \propto T$ setzt, so erhält man mit
\begin{align*}\rho \propto \Omega^{2/3} \sqrt{T}\end{align*}
etwas, was der Erfahrung nicht entspricht. Diese entsprach vielmehr einer von W. Wien 1913 aufgestellten Hypothese: $v$ ist temperaturunabhängig, und der "Wirkungsquerschnitt" $\sigma^2 = 1/nl$ ist nicht der Querschnitt eines Atoms sondern ein durch die Wärmeschwingung der Atome bedingter zusätzlicher Querschnitt ($\propto T$). Beides konnte 15 Jahre später aus der Quantentheorie geschlossen werden.
Die etwa 1927 vollendete Quantentheorie brachte zwei entscheidende Neuigkeiten. Die Unteilbarkeit des Wirkungsquantums $h$ ergab die quantentheoretische Unbestimmtheit, den Dualismus Welle-Teilchen, das Übergreifen der Wellenfunktion in benachbarte Potentialmulden, den "Tunneleffekt". Die Unteilbarkeit des Elektrons bedeutete die Ununterscheidbarkeit von Elektronen und die Fermi-Statistik. Für die Stoffeigenschaften sind beide Züge wichtig. Die aus dem erstgenannten Zug folgenden diskreten Energiezustände eines Atoms sind wegen des zweiten Zuges bis zu einer Stelle besetzt. Bei einer Molekel aus zwei gleichen Atomen sind wegen des zweiten Zuges die Energien paarweise geordnet. Bei einer Anhäufung von $N$ gleichen Atomen entstehen Gruppen von je $N$ Energiewerten; bei einer unendlichen periodischen Folge gleicher Atome entstehen "Energiebänder" einfacher Struktur, die bis zu einer Energie $\zeta$ besetzt sind (Abb. 2).
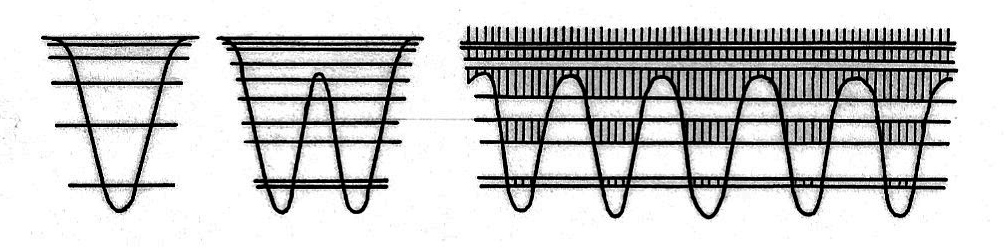
Bei "Valenzstrukturen", wie Molekelgitter oder Diamantgitter, fällt $\zeta$ in eine Bandlücke, man erhält im Idealfall einen Isolator (oder bei schmaler Lücke einen Halbleiter); bei "dichten Packungen" erhält man metallische Leiter.
Die einfache Widerstandsformal
\begin{align}\rho = \frac{m\ v}{e^2 n l} \propto v\ \sigma^2\end{align}
gilt auch in der Quantentheorie, $v$ ist jetzt die temperaturunabhängige Geschwindigkeit an der Fermi-Grenze $\zeta$ und $1/nl$ bezeichnet jetzt die Abweichung von der Periodizität des Kristallgitters. Bei Baufehlern ist
\begin{align*}\sigma^2 \propto n_F\end{align*}
proportional der Anzahl der Fehlstellen in der Raumeinheit; infolge der temperaturbedingten Schwingungen kommt (bei nicht zu tiefen Temperaturen)
\begin{align}\sigma^2 \propto T/M\ \omega^2\end{align}
hinzu, wo $M$ die schwingende Masse $\omega$ eine mittlere Frequenz der Schwingung ist. Nach dieser einfachen Vorstellung ist der elektrische Widerstand ein Ausdruck der Baufehler und der elastischen Eigenschaften des Metallgitters.
Wir haben jetzt zu prüfen, ob neben Baufehlern und elastischen Eigenschaften noch andere Züge der Elektronenstruktur, die man qualitativ als größere oder geringere "Freiheit" der Elektronen bezeichnen kann, mitwirken.
In atomaren Einheiten reduzieren sich (4) und (5) auf
\begin{align*}\rho = \frac{v\ T}{M\omega^2}\end{align*}
Die Fermistatistik ergibt $v$ umgekehrt proportional zum Atomabstand, in atomaren Einheiten
\begin{align*}v = \Omega^{-1/3}\end{align*}
dimensionsmäßig wird ($M \omega^2$ ist Energie:Länge²):
\begin{align*}M \omega^2 = \Omega^{-1}\end{align*}
sodaß wir
\begin{align}\rho = \Omega^{2/3}\ T\end{align}
erhalten. Dabei mögen noch Faktoren zwischen 1 und 10 stehen. Die Temperaturabhängigkeit ist bei nicht zu tiefen Temperaturen empirisch bestätigt. Die Tabelle vergleicht den so errechneten Widerstand mit dem bei Zimmertemperatur, $T = 10^{-3}$ (in atomarer Einheit), gemessen.
| \begin{align*}\Omega\end{align*} | \begin{align*}\Omega^{2/3}\ T\end{align*} | \begin{align*}\rho_{\rm emp}\end{align*} | |
| Na | 270 | 0,04 | 0,2 |
| Ag | 116 | 0,02 | 0,07 |
Die Dimensionsbetrachtungen geben also die richtige Größenanordnung.
Daß die Widerstände gerade wenig unterhalb der atomaren Einheit liegen, kommt daher, daß großes Atomvolumen und niedrige Temperatur einander entgegenwirken.
Statt durch das Atomvolumen können wir das elastische Verhalten durch die (den Verlauf der spezifischen Wärme kennzeichnende) "Debye-Temperatur" $\Theta$ ausdrücken. In atomaren Einheiten ist
\begin{align*}\Theta = \omega\end{align*}
also
\begin{align*}\rho = \frac{T}{\Omega^{1/3}\ M\Theta^2}\end{align*}
Rechnet man danach das Verhältnis der Widerstände von Na und Ag aus, so bekommt man 6 bis 7, statt 2 der obigen Tabelle; in Wirklichkeit ist es 3.
Ag leitet besser, weil es "steifer" ist, aber doch nicht so gut, als der Steifheit entspricht.
Wir betrachten jetzt im einzelnen die empirische Korrelation zwischen Atomvolumen $\Omega$ und Widerstand $\rho$.
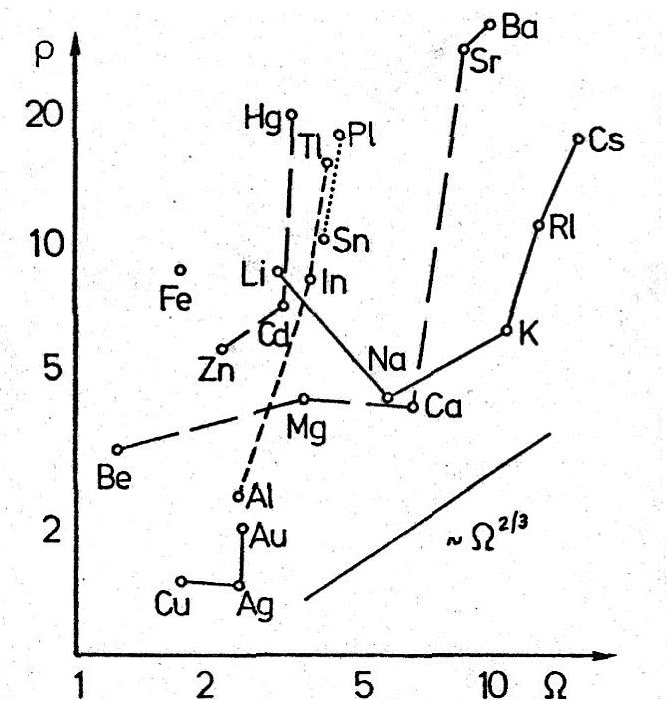
In Abb. 3 sind für eine Anzahl chemischer Elemente diese Größen in logarithmischem Maßstab und willkürlichen Einheiten angegeben. Die Beziehung $\sigma\propto\Omega^{2/3}$ erscheint jetzt als Grenze, rechts und unterhalb derer nichts vorkommt; was weiter links oberhalb liegt, zeigt eine "Unfreiheit" der Elektronen an.
Die einwertigen Elemente Na, K, Rb, Cs zeigen qualitativ die Zunahme von $\rho$ mit $\Omega$. Cu, Ag, Au leiten besser, weil die Atome kleiner sind, aber darüber hinaus noch etwas besser, weil ihre Gitter verhältnismäßig steif sind. Cu und Au leiten dabei verhältnismäßig schlechter als Ag, sie sind auch weniger einwertig als Ag. Wir bemerken eine gewisse Unfreiheit der Elektronen bei Cu, Au, Li, Rb, Cs. Die zwei- und dreiwertigen Elemente leiten, als hätten sie nur ein Elektron je Atom oder schlechter. Die Zahl der Valenzelektronen zeigt sich nicht, sie wird irgendwie durch deren Unfreiheit kompensiert. Das zeigt sich auch bei Sn und Ph, noch stärker bei Fe.
Die Elektronenstruktur eines Atoms wird in der Ein-Elektron-Näherung durch die Energiewerte $E(n,l)$ der einzelnen Elektronen ausgedrückt; besonders wichtig sind die in der Nähe. der Besetzungsgrenze $\zeta$ liegenden. Die Elektronenstruktur in einem Kristallgitter wird durch die Funktion $E$($n$,$k$) ausgedrückt, wo $k$ der Wellenzahlvektor ist. $E(k)$ ist periodisch mit den Perioden des reziproken Gitters. Bei den Metallen ist die Fläche $E(k) = \xi$ im Wellenzahlraume, die "Fermi-Fläche" wichtig.
Die einwertigen Metalle Na und K haben fast kugelförmige Fermi-Flächen, die Elektronen verhalten sich fast wie freie Elektronen. Rb, Cs zeigen kleine Abweichungen von der Kugel, Li ebenfalls. Die Fermi-Flächen von Cu, Ag, Au bestehen aus Kugeln, die periodisch im $k$ Raum angeordnet und durch enge "Hälse" miteinander verbunden sind; bei Ag sind die Hälse am dünnsten. Wir sehen also bei den einwertigen Metallen qualitativ eine Korrelation zwischen Fermi-Fläche und Widerstand.
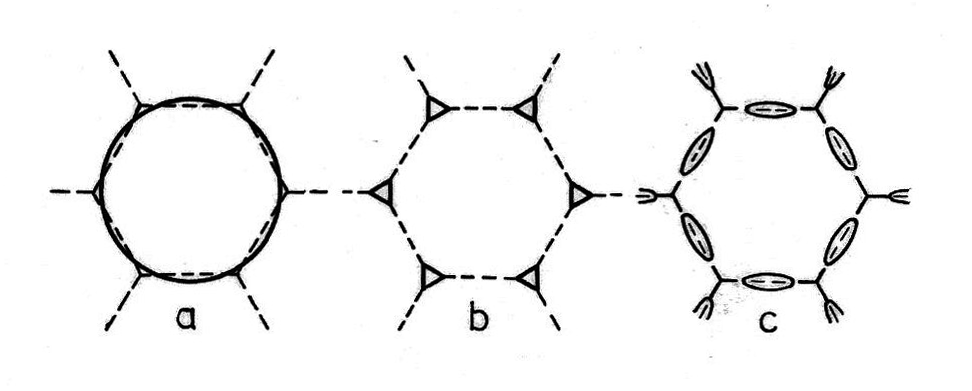
Bei den zweiwertigen Metallen kann man nicht von genähert freien Elektronen sprechen. Im gedachten Grenzfall starker Bindung der Elektronen an die Atomreste haben wir abgeschlossene $s^2$-Schalen, also Isolatoren. In der Näherung freier Elektronen unter Berücksichtigung der periodischen Wiederholung von $E(k)$ erhalten wir kleine Fermi-Flächen. Abb. 4 gibt diese im zweidimensional vereinfachten Modell wieder; im ersten Band sind alle ??-Stellen bis auf die kleinen Gebiete besetzt; im zweiten Band sind nur die kleinen Gebiete besetzt. Die zweiwertigen Metalle sind "beinahe Isolatoren". Empirisch leiten Mg und Ca noch verhältnismäßig gut, die anderen leiten schlechter. Auch Zn, Cu und (festes) Hg weichen stark vom Verhalten freier Elektronen ab. Zwischen den besonderen Verhältnissen der feinen, zierlichen Fermi-Flächen und dem elektrischen Widerstand besteht keine deutliche Korrelation.
As, Sb, Bi sind ihrer Gitterstruktur nach "Halbmetalle, beinahe Isolatoren"; sie haben auch große spezifische Widerstände.
Grob qualitativ verstehen wir den elektrischen Widerstand der Metalle als Folge der elastischen Eigenschaften, modifiziert durch die Elektronenstruktur. Aber der elektrische Widerstand (ohne Magnetfeldeinfluß) ist sicher kein geeignetes Mittel, die Gestalt der Fermi-Fläche zu erforschen.
Blicken wir auf die seit Ohms Entdeckung verflossen Zeit zurück:
Vor 150 Jahren wurde das Ohmsche Gesetz entdeckt,
vor 75 Jahren das Modell der Elektronen mit begrenzten Weglängen gefunden,
vor gut 60 Jahren wurden wesentliche Züge der Elektronenleitung erkannt,
vor 50 Jahren wurde die Quantenmechanik geschaffen, die besonders mittels der Schrödinger-Gleichung eine Theorie des elektrischen Widerstandes ermöglichte,
vor 20 Jahren lebte die "Fermiologie" auf, die Erforschung der Fermi-Flächen.